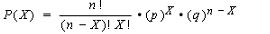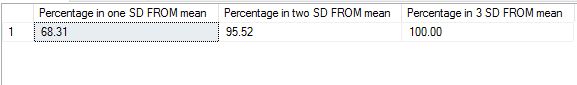As some readers may know, I am a regular attendee on SQL Cruise s for 8 years now. SQLCruise is a training(&-vacation for some) event organized by Tim Ford(b | t ) and Amy Ford (t) that happens twice a year. I went on the first one on Alaska 8 years ago – and I have been hooked since then doing them. I go on atleast one cruise every year – usually the one closest to the east coast. This year the route happened to be around western carribean – including 3 countries I had not visited before – Honduras, Mexico and Belize. Well, the third didn’t quite happen but the other two did and was a ton of fun. My notes are as below. I use this as a way to plan better for next year , so many things I have written are only relevant to me, and perhaps to other frequent cruisers. If you find them too rambling skip all the way down to the ‘Takeaways‘ section where I have summarized the value and gains I get from doing this.
Day 0: I landed in Miami, our port city, late on Thursday January 26th. I have learned the hard way to fly in atleast one day early before the cruise ship leaves – because of frequent and unexpected flight delays, especially in winter. This year was an unusually warm winter with no weather related delays. I did however, manufacture some stress for myself (am seriously good at this) because of a short layover time of 45 minutes at Charlotte. Thankfully, I made the connection, with my luggage intact and checked in into the Hilton, where most of the other cruisers were staying. This is yet another lesson learned over the years – staying with everyone else at the same hotel before takeoff adds some good energy and reduces nervous tension. There is somewhat of a tradition around having breakfast together and leaving in vans to the terminal to board – there is a very comfy, family-like feel to that which is, to me, worth the extra $$ it might cost to stay at a hotel like the Hilton. I spent the next day just wandering around downtown Miami – it was too overcast and rainy to go to the beach.I walked around, got myself some good food to eat at the huge Whole foods Market, napped and waited for the rest of #sqlfamily to arrive.
Day 1: A number of cruisers, most of us known to each other fairly well – met up at the breakfast buffet early. After a heavy, hearty meal (which is needed since boarding and getting food on the ship can take some time) – we piled into a couple of uber taxis and made our way to the cruise terminal. I got to meet one of the new tech leads and new cruiser – Ben Miller and his lovely wife Janelle. We stood in line together and were checked in rather quickly. I was handed my room keys and found to my pleasant surprise that I was on the 5th floor. I was just one floor away from classroom on the 6th and one floor away from dis embarking when ship docked. This was so much easier than being up on 11th or 12th and waiting endlessly for elevators to arrive. My room was also much more airy and brighter than the small cubby-hole kind of rooms I had used before (I paid more for it and my co passenger/sister could not make it). Although it was expensive it seemed very worth it.I made my way to lunch buffet for a quick bite, and then joined the classroom shortly after. There were many former cruisers I knew rather well – Joe Sheffield, Jason Brimhall, Bill Sancrisante, Erickson Winter, Ivan Roderiguez – and among tech leads Ben Miller (b|t) , Jason Hall(b|t), Grant Fritchey(b|t), Kevin Kline(b|t) and Buck Woody(b|t). The rest of the day was taken with exchanging pleasantries, meeting families and getting the week started. We were handed our swag – which was seriously awesome this time. The timbuctoo back packs are always great, as well as soft cotton t shirts – but my favorite was the water bottle/flask.
Day 2: This was a day at sea. The day started with Buck Woody’s session on Data Pro’s guide to the Data Science path. As someone who did a career change from 20 years of operational dba work into BI/Analytics – I found it very interesting. Buck went through an introduction to data science and R programming, various tasks involved in data science profession, and most importantly – how a regular database person can break into this field. The presentation was among the most pragmatic, useful ones I have attended on this subject. Buck also spiced it up with his own brand of humor, small quizzes and exercises – which made it extra interesting. Following this session we had Grant Fritchey’s session on row counts, statistics and query tuning – for anyone doing query tuning on a regular basis, this information never really gets old and is worth listening to every single time. Grant covered changes to optimiser on SQL Server 2016 as well. Following lunch, we had a deep dive/500 level session by Kevin Kline on Optimizer secrets and trace flags. Kevin had a ton of information packed into a 1.5 hour session. The day ended with a group dinner at a restaurant. I personally never have much luck with ship’s restaurants given the restrictions on what I can eat – this time was not any different. I had great company though, to keep me entertained throughout – Buck Woody with his wife and mom, Chris and Joan Wood. I hugely enjoyed chatting with them and getting to know them better. I ended the day by grabbing a bite to eat at the buffet that suited my palate and retired, happy and satisfied.
Day 3: This was a day at port at Roatan Islands, Honduras. We had time for a quick class on encryption by Ben Miller. Ben’s presentation was simple and clear with great demos. Following this we docked at Roatan Islands. I was taking the ship’s tour to Gumbalimba Animal Preserve. I was very happy to have Chris and Joan Wood for company. I love sightseeing, it is one of the reasons for me to do sql cruise – and having company on those tours make them more fun and worth doing. It was a rainy, overcast day – we were taken on a bus ride to the park, which housed a lot of extinct animals and birds. It was a lush, green paradise. We got to play with macaws, white faced monkeys, take a lot of fun pics and returned late afternoon. It was a very fun day, despite the rain.


Day 4: We were supposed to be docked at Belize. But captain announced that they had some unexpected hurdles that prevented them from doing so, and that this would be a day at sea. I have not seen this happen on any other cruise I have been on before. I wondered how to spend the day. Tim got us together, and asked if we’d like to hear more on tools from Red Gate and SQL Sentry – two of the key sponsors. Almost every place I’ve worked at have used these tools, and I thought it was a great idea. The team seemed to agree. We spent the day at class – listening to some great tips and tricks on Plan Explorer and various Red Gate tools. To be honest this unexpected day was my highlight of the trip – I got great tips on tools I use, and I spent a very relaxing day discussing them among friends.
Day 5: We docked at Costa Maya, Mexico. I had booked a tour of mayan ruins that I wanted to see with fellow cruisers. We had to set the clock back a day ago because of a time zone change. There was another notification to set it forward for today, which I missed reading. So I showed up an hour late for the tour and they had already departed. I was very disappointed. The ship’s cruise excursions team was kind enough though, to refund the money to me since it was a genuine mistake. I spent the money on some lovely handicrafts near the port, took a long walk by the beach, got back in boat early, and took a nice nap. So in all, although things did not go per plan exactly, it turned out quite well. Towards the end of the day, we had a tech panel discussion with all the tech leads – a lot of interesting questions were posed and answered.

Day 6: We docked at Cozumel, Mexico. I left the boat early and joined fellow cruisers for a tour of Mayan ruins. It was a long bus ride to the spot, and a good two mile walk in hot, humid weather. We did get a good look at ruins (one thing off the bucket list), spent some time on the lovely beach there and got back to the ship by mid afternoon. We had a second group dinner at night – with some good conversation.
Day 7: There were several classes this day – by Grant, Buck, Ben and Jason Hall. It is hard for me to say which one I liked the most. Since am into BI and Analytics – Buck’s session on R had me listening with total attention .I liked the many examples and the differences illustrated between SQL and R programming. Although I have done both and know them rather well, I have always had a hard time explaining this to other people. Buck did a fantastic job and I will use his examples for this purpose. All other sessions were great in quality too. The day ended like it usually does with a group social, lots of pictures taken, hugs and fond messages of regard. Every cruise to me has been worth it for this time, but this particular one had a lot of people with a lot of affection going around , and made it extra special.

Day 8: There is not much here to say except some lessons learned after several years of cruising. I booked a late flight hoping that I could hang out on the ship until lunch – turned out that everyone had to be out by 10 AM. I also made the mistake of opting for the ship’s shuttle thinking I could save on uber/taxi – this means you are mandated to check in luggage, not take it with you. There were other cruisers taking a shared ride and I could have joined them instead of checking luggage, but was too late. After a quick and early breakfast with Kevin Kline, Lance Harra and Jason Hall – I walked down the ship, into and past customs and into the luggage area. There was a 1.5 hour wait in a cold and dark room for luggage to arrive here, and when it did it was in another adjacent room. Lance and myself had to ask to find out where it was. This is definitely something to avoid next time. At the airport – I had a long 8 hour wait for my flight. Kevin Kline checked me along with Jason and Lance into the American Airlines exec lounge for the day. Kevin does this for me and fellow cruisers every year – a kindness that I appreciate very much. I could nap in the super comfy lounge, get a salad for a meal and then walk out when it was closer to boarding time – seriously better than wandering around in the airport. My flight was on time and I reached home safe.Another note for next year is to take the following day off from work. I was bone tired and had to go in. Things settled down over the week but that would have been a welcome day off.
So…after all this rambling..what did I come away with? My key takeaways from this particular cruise are as below:
1 How to get into data science? : I learned from Buck Woody’s sessions on how a data professional like me can make my way eventually into data science. Working on data cleansing and learning visualisation skills are important, and it was very beneficial for me to learn that. There are a lot of rumors/myths and false information around on data science – every second person you meet who is a data professional wants to get into it. But to get real practical advice from people who got there , and people who have SQL server as their background – is hard to get anywhere else.
2 Tools and more tools…: The day spent discussing tools was unique, wonderfully informative and fun. The only time anyone gets to hear such sessions are occasionally at sql saturday vendor sessions – I must be honest here that I have never really attended any of them. This was unique in that every person asked questions on these tools, enhancements they’d like and various ways they used them. Grant Fritchey, Kevin Kline and Jason Hall did a great job fielding these questions. I felt that my day was well spent ,what I said was heard and would go into some future version of Red Gate and Sentry one tools.
3 What to learn besides sql server? – There are big changes happening in the data industry – everyone knows we need to have more than sql server on our resume. But nobody really knows what that ‘more’ needs to be or where it is going to get us. I heard from so many fellow data professionals – some were learning unix, some were into Azure/cloud in a big way and also exploring AWS and other cloud services, some were doing R programming and data analytics..on and on. It was enriching and heart warming to hear of each person’s experience and where it was taking them. It gave me confidence that I was not alone, and also a good idea of what are skills most people are looking to gain as the industry expands.
Last but not the least – I am not a naturally extroverted person. I do well in small, familiar crowds of people but am seriously shy among larger audiences. SQL cruise has really taught me to open up, be more relaxed even among strangers and speak to the technical info that am familiar with. I met several new people on this trip whose friendships I will treasure- Derik Hammer (t), Chris Wood (t) , Lance Harra(t), Kiley Pollio, Joe Fullmer and Brett Ellingson. I apologize for missing anyone, it is not intentional and your company was wholly appreciated.
I am already looking forward to the next one in 2018!! THANK YOU to Tim and Amy Ford, Red Gate and Sentry One, and all tech leads for making it a pleasant, valuable experience.
:

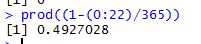
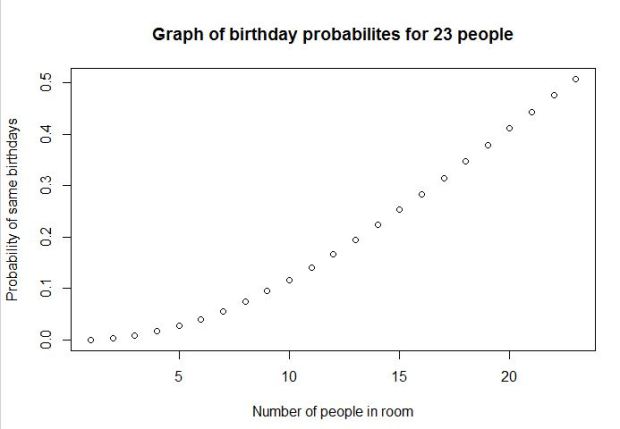
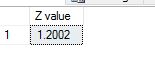
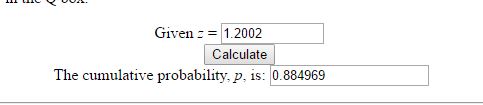
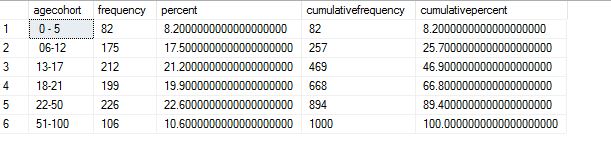
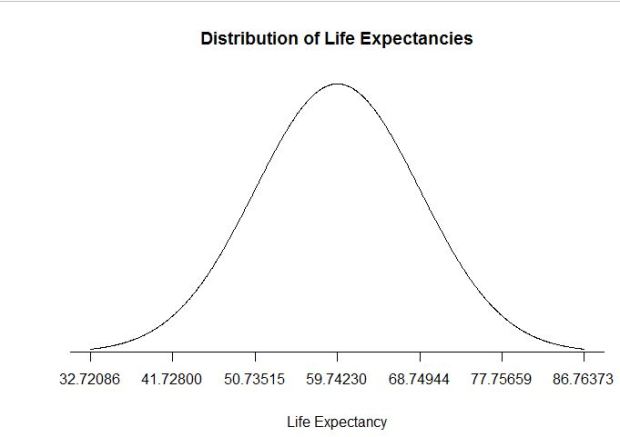
 where ‘meu’ in the numerator is the mean and sigma, the denominator is the standard deviation. Let us use some tried and trusted t-sql to arrive at this value.
where ‘meu’ in the numerator is the mean and sigma, the denominator is the standard deviation. Let us use some tried and trusted t-sql to arrive at this value.