The Birthday Problem – with T-SQL and R

When I was on SQLCruise recently – Buck Woody (b|t) made a interesting statement – that in a room of 23 people, there is over a 50% chance that  two or more have the same birthdays. And sure enough, we did end up having more than two people with same birthday. I was tempted to play with this rather famous problem (there is a great introductory wiki post on it here)  using statistics for a while, and got around to it this weekend. Let us test the hypothesis first.

Given a room of 23 random people, what are chances that two or more of them have the same birthday? 

This problem is a little different from the earlier ones, where we actually knew what the probability in each situation was.

What are chances that two people do NOT share the same birthday? Let us exclude leap years for now..chances that two people do not share the same birthday is 364/365, since one person’s birthday is already a given. In a group of 23 people, there are 253 possible pairs (23*22)/2. So the chances of no two people sharing a birthday is 364/365 multiplied 253 times. The chances of two people sharing a birthday, then, per basics of probability, is 1 – this. Doing the math then – first with T-SQL –

DECLARE @x INTEGER, @NUMBEROFPAIRS INTEGER, @probability_notapair numeric(18, 4), @probability_pair numeric(18, 4)
DECLARE @daysinyear numeric(18,4), @daysinyearminus1 numeric(18, 4)
SELECT @x = 23
SELECT @numberofpairs = (@x*(@x-1)/2)
SELECT @daysinyear = 365
SELECT @daysinyearminus1 = @daysinyear - 1

SELECT @probability_notapair = (@daysinyearminus1/@daysinyear)

SELECT 'Probability of a pair having birthdays' ,1-power(@probability_notapair, @NUMBEROFPAIRS)

In R this is very easily calculated using the line

prod(1-(0:22)/365)

To be aware that prod is just a function that multiplies what it is supplied, it is not a special statistical function of any kind. In this case since the math is really easy, that is all we need to calculate the result.

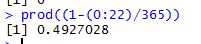
As we can see it is pretty close to what we got with T-SQL.

We can play around with R a little bit and get a nice graph illustrating the same thing.

positiveprob <- numeric(23) #creatingvectortoholdvalues
#loop and fill values in vector
for (n in 1:23) {
 negativeprob <- 1 - (0:(n - 1))/365
 positiveprob[n] <- 1 - prod(negativeprob) }
#draw graph to show probability
plot(positiveprob, main = 'Graph of birthday probabilites for 23 people', xlab = 'Number of people in room', ylab = 'Probability of same birthdays')

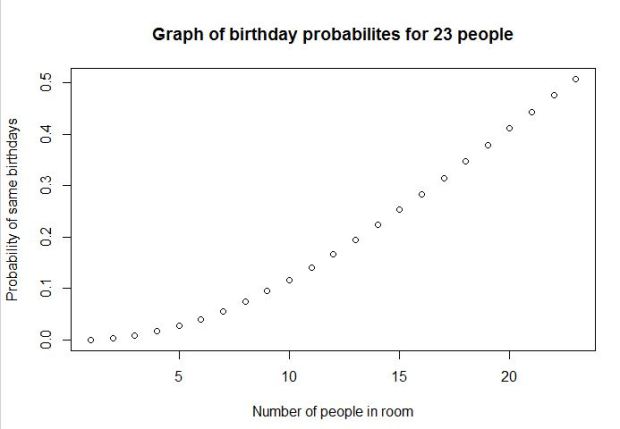
As we can see the probability of two or more people sharing a birthday in a room of about 23 is near 50%. Pretty amazing.

There is a ton of very detailed posts on this rather famous problem, this is just a basic intro for those of you learning stats and R.
1 https://www.scientificamerican.com/article/bring-science-home-probability-birthday-paradox/

2 http://blog.revolutionanalytics.com/2012/06/simulating-the-birthday-problem-with-data-derived-probabilities.html

Thanks for reading!!